吴式枢（1923—2009），江西宜黄县人。理论物理学家，吉林大学物理系和理论物理专业的主要创建者。1980年当选为中国科学院学部委员（院士）。1944年毕业于上海同济大学机械工程系。1948年在美国伊利诺斯大学获硕士学位，1951年获博士学位后回国。历任大连工学院教授，吉林大学教授、物理系主任、名誉系主任，吉林大学自然科学学术委员会主任。曾任国务院学位委员会第一、第二届学科评议组成员；中国核物理学会副理事长；吉林省科学技术协会副主席、学术委员会副主任；吉林省物理学会理事长、名誉理事长。他在应用格林函数方法研究核多体问题上开展了多方面的系统研究，最早在格林函数中引入非线性积分方程，阐明了非线性积分方程在格林函数中的物理含义及应用；建立了一种获得格林函数积分方程核的严格封闭表达式的方法；提出了一个将四维相对论性二体波动方程严格化为三维形式的方法，推导出了相对论性无规位相近似的完整表达式，给出了相对论性Hartree-Fock近似的重整化方法。有关研究成果获1978年全国科学大会奖，1982年国家自然科学三等奖，2005年何梁何利科学成就奖。1990年被国家教委和国家科委联合授予“全国高等学校先进工作者”称号。 

一、生平概要

吴式枢祖籍江西省宜黄县，1923年5月27日生于北京，2009年2月27日在长春病逝，终年86岁。

1936至1939年就读于上海同济大学附属高级中学，1944年于上海同济大学机械工程系毕业后留校任理学院助教。1947年秋赴美国伊利诺斯大学研究院攻读理论物理，师从S.M.Dancoff教授，1948年获科学硕士学位，1951年获哲学博士学位。他原准备继续留在美国一、两年做些研究工作以进一步充实自己，但因不满美国操纵联合国通过诬蔑我国为侵略国的决议，觉得他们有侵略我国的野心，想起耳闻目睹的旧中国在国际上那种没有地位、受人欺辱的情景，他的心情就难以平静，对新中国寄予了无限的希望，获得博士学位后，他立即响应周总理对海外科学家的号召，抱着要为祖国尽快强威起来尽力献身的夙愿，谢绝了导师的挽留，也不顾父亲亲自从台湾赶到香港来一再劝阻，毅然回到了诞生不久的新中国，投身于祖国的教育科学事业。

1951年10月起任大连工学院应用物理系教授，1952年9月在全国高等院校调整中调入东北人民大学（现吉林大学）物理系任教授，参与物理系的创建，1955~1957年任物理系副主任，1957~1984年任系主任，1984年后任名誉系主任。1958年还亲手创建了理论物理专业。曾任吉林大学自然科学学术委员会主任。

曾任国务院学位委员会第一、二届学科评议组成员；中国核物理学会副理事长；吉林省科学技术协会副主席、学术委员会副主任；吉林省物理学会理事长、名誉理事长。

1978~2002年他是5~9届全国人民代表大会代表。 

二、学术生涯

吴式枢在大学阶段长期学的是工程机械，在学期间他对社会活动和人际交往不感兴趣，觉得以后若从事工程技术工作难免要与多个部门的人员打交道，自己缺乏这方面的能力，因此大学毕业后他就自学物理学，希望日后能与世无争地专心从事学术研究。

在美国攻读博士学位期间，他于1951年在美国《物理评论》（Phys.Rev.）上发表了他的第一篇论文“对常规摄动理论的评注”（A remark on the conventional perturbation theory）。1951年9月他以“应用独立粒子模型讨论轻核的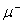捕获和光核反应”（A discussion of the nuclear 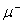-capture and photonuclear effect for light nuclei by the individual particle oscillator model）获伊利诺斯大学哲学博士学位，他的博士论文以单行本形式寄送有关单位。在博士论文中他把刚刚提出的原子核壳层结构模型应用于研究轻核的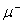捕获和光核反应，推导出了相关的共振峰公式，此成果当时被称为Wu(吴)模型。

1955年，在戴逊（Dyson）铁磁理论发表之前，吴式枢就讨论了两个自旋波函数系统，用它们组成新的线性波函数，消除了布洛赫（Bloch）理论中过多本征态的困难，这是铁磁理论发展中的一个重要的阶段性成果。

1962~1966年，吴式枢对处理原子核基态关联效应的无规和高阶无规位相近似（RPA—HRPA）的理论基础进行了研究，他用变分法推导出该方程，从而自然地给出了一种使RPA和HRPA方程具有厄米性的途径，保持厄米性是物理学所要求的。他还应用格林函数方法推导出HRPA的久期方程，据此对它进行了费曼（Feynman）图解分析，深化了对HRPA的认识。在上述工作基础上，他提出了“推广的组态混合法”，给出了用它求解实际问题的途径，此成果在1966年北京科学讨论会上报告后得到了国内外同行的好评。

1970年代，吴式枢最早在格林函数中引入非线性积分方程，于1973年、1974年分别在《中国科学》上发表了 “非线性积分方程与格林函数方法—粒子-空穴相互作用的无规位相（RPA）自屏蔽”I和II两篇重要论文。文中阐明了非线性积分方程在格林函数理论中的应用及其物理含义，指出通过格林函数的非线性积分方程不仅可以自动地产生无穷多个不重复的不可约顶角，还可以同时求得由这无穷多个不可约顶角所产生的各级Feynman图之和，是个非常有效的计算手段。作为举例，文中对粒子-空穴格林函数建立了一组非线性积分方程，证明其解包含了粒子-空穴相互作用的所有各级无规位相（RPA）自屏蔽所引起的重整化效应。非线性问题正越来越受到人们的重视，随着对物理问题探索的不断升如何处理非线性方程数学手段的不断完善，可以预期，格林函数的非线性积分方程将越来越广泛的得到应用。1981年初，联邦德国洪堡基金会主席、土宾根大学理论物理研究所所长、国际著名理论核物理学家费茨莱（Faessler，A）教授在北京核物理讲习班上作关于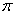凝聚问题的特邀报告时，特别提到有一个问题尚未找到解决的办法。其实他提的这个问题正可以用吴式枢提出的格林函数的非线性积分方程来解决，当他在会下得知这一情况后，对吴式枢教授的这一成果极感兴趣，当即表示愿与吴式枢合作。半年后他就邀请吴式枢到他的研究所去讲学和开展合作研究，并把吴式枢教授作为访问联邦德国的著名外国学者在报刊上作了专门介绍。这值得一提的是，吴式枢这两篇论文的雏形实际是在“文化大革命”期间他遭遇不公正对待，被隔离审查，已失去正常工作条件的时候开始孕育形成的，当时他仍坚信自己回国献身于祖国的科学教育事业没有错，他仍在用脑子思考着他的科学问题。

由单粒子位阱代表的平均场不仅决定了核的零级近似波函数，而且关系到核的等效相互作用及其所引起的多体关联效应，因此单粒子位阱的研究一直是多体理论研究的一个重要方面。从1970年代后期起，吴式枢利用格林函数方法对通过质量算符M定义的单粒子位阱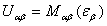进行了系统研究，广泛应用的Hartree-Fock单粒子位阱是质量算符的最低级近似。吴式枢证明了由质量算符定义的单粒子位阱虽然是非厄米的，但由它所确定的分立本征值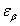一定是实的，而且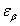严格等于满壳层基态与其相邻核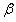态的能量差，其本征函数满足一类最大重叠原理；此单粒子位阱具有最佳的抵消性，能最大限度地抵消掉由二体相互作用产生的Feynman图，从而可使单粒子格林函数的表达式得到简化，使其计算变得更为容易和精确；说明它是单粒子位阱的一种好选择。通过二能级Lipkin模型和推广的三能级可解模型验证了上述一般性结论。

应用格林函数的关键是要写出它的不可约顶角算符，按通常的摄动方法只能写出他顶某些低级近似。1986年吴式枢在“计算温度2t格林函数的一个系统方法”（A systematic method for the calculation of temperature 2t Green’s function）一文中，从格林函数的运动方程出发，提出了一种推导零温和有限温双时格林函数不可约顶角的系统方法，给出了它的严格表达式，由此表达式可按摄动方法方便地对它进行逐级计算。作为举例，文中给出了有限温粒子-空穴格林函数的不可约顶角算符直至二级的具体表达式。在实际应用中往往只能或只需要在某一较小的模型空间内讨论问题，吴式枢和郭子斯（T.T.S.Kuo）还推导出了在模型空间里的格林函数的等效积分方程，给出了计算等效顶角算符的一般公式。

从1980年代后期起，吴式枢将研究重点转向相对论性多体理论和量子强子动力学（QHD）的研究。相对论多体方程是相对论多体理论的基础，虽然已经有一种严格的相对论束缚态的多体方程—Bethe-Salperter（BS）方程，但由于该方程存在闵氏时间而使问题大大地复杂化了，甚至会产生某些非物理解，再加上方程本身是个维数为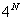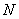（为体系所含的粒子数）的联立方程组，求解极为困难。人们曾用瞬时近似、准势近似等方法来消除时间变量将该方程三维化，这些近似都不可避免地忽略了一些重要的相对论效应。对为何建立严格的与B-S方程等价的三维相对论性方程，曾有一些探讨，但均未能找到恰当的办法给出方程中相互作用核的明显表达式。1990年，吴式枢在“三维相对论性二体波动方程”（Three-dimensional relativistic two-body wave equation）一文中利用格林函数方法重新导出了三维相对论性二体波动方程，给出了关于按Feynman规则进行计算的严格表达式，为相对论性波动方程的实际应用提供了一个很好的理论框架。1992年，吴式枢等在“相对论性无规位相近似的严格谱表示”（A rigorous spectral representation of relativistic random phase approximation）一文中，从所建立的严格三维相对论性二体波动方程推导出相对论性无规位相近似的严格谱表示，不仅给出了直接作用项，还能自然地给出国外相应工作不能给出的交换作用以及推迟效应项。利用所推导出的相对论性RPA谱表示，吴式枢及其合作者对轻核能谱及核物质的结合能、饱和密度以及不可压缩系数进行了相对论性计算，采用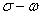介子交换模型考察了粒子-空穴关联、推迟效应、核的有限尺度以及单粒子基的选择对计算结果的影响，发现这些因素的影响是不能忽略的，从而肯定了核物质和有限核进行相对论性研究的必要性。吴式枢还指出自洽的Hartee-Fock重整化可简化为自洽的Fock重整化；给出了关于自能的四维表示和三维表示之间的相互关系以及子能的封闭的三维表达式；提出了一个克服相对论性Hartree-Fock近似所存在的重整化困难的方法，建立了一套可付诸实施的重整化方案；他及其合作者考察了自洽效应及自洽条件对重子传播子、介子传播子性质所产生的影响，研究了鬼点消除对自能性质的影响。

可以说在核多体理论语格林函数方法方面，吴式枢有多方面的创造性的建树，已形成了独具特色的理论处理方法。

吴式枢是从事基础理论研究的，但他也关心国家建设的当前需要。1971年在下厂调研中，他了解到大庆油田在开发中急需解决水淹油层的判断问题，传统的电阻率测井在这方面往往无能为力。回校后他就带领一个课题组，并联合数学系的老师参与，发挥理论物理专业的优势，在很短的时间内提出了通过高频电磁波传播的相位差测量来确定地层介电常数以判断水淹油层的方案，为大庆油田研制XJC相位介电测井仪以及相关的测井资料解释提供了物理基础和仪器设计依据（我国是继苏联之后第二个在石油测井中开展介电测井研究的国家），也使吉林大学理论物理专业由此开辟了一个应用基础研究的方向，建立起电法和声法测井科研组，做出了一批水平较高的科研成果，培养了一批石油测井理论方法方面的高级人才。1970 年代中期，为适应我国核科学和核工业发展的需要，国家组建了核数据中心，吴式枢又带领一些同志承担了轻核中子反应数据的理论计算工作，为我国核数据库的建立和发展做出了贡献。

2005年吴式枢获何梁何利科学成就奖。在科研事业上能取得这样丰硕的成果，是他长期探索、严谨治学的结果，这里面饱含着他对科学真理的执著追求，也凝聚着他为祖国的繁荣昌盛献身的赤诚之心。正如他在“自述”中说的：“我已平淡而从容地度过了几十个春秋，正如一个平凡的人过着平凡的生活。如果说我获得了一些收获，那么耕耘着它们的就是一个明确的人生目的，一份无论在顺境或逆境中都能坦然面对现实、不忘敬业根本的执着和一种持之以恒的勤奋。”

吴式枢是兰州重离子加速器国家重点实验室原子核理论研究中心科学顾问，是中国科学院高能物理所、上海原子核研究所的兼职研究员，曾任中国科学院理论物理研究所学术委员。他理论基础深厚而又诲人不倦，他严谨治学的学风在国内理论物理同行中得到很高的评价，同行们都把他当作良师益友，愿意和他讨论问题，每次参加学术会议，他的周围常聚集着许多中青年学者，平时也常有人专程到长春来向他求教。

1980年吴式枢作为中国代表团团长率团参加了在美国举办的“国际第三次核物理会议”，多次作为中国代表团成员参加了中美、中日以及海峡两岸的核物理学术交流活动。他作为组织委员会主席之一，分别于1983、1986、和2001年组织了在长春举办的“核子-核子相互作用与核多体问题”、“核相变与重离子反应”、“核多体问题与核的子核自由度”国际暑期讲习班，为我国的核物理界与世界的学术交流做出了贡献。 

三、主要的学术成就

1. 最早在格林函数中引入非线性积分方程，该方程不仅可自动地产生无穷多个不重复的不可约顶角，还可同时求得由这无穷多个不可约顶角所产生的各级Feynman图之和。

2. 提出了一种推导零温和有限温双时格林函数不可约顶角的系统方法，给出了它的严格表达式，利用此表达式可按摄动方法对它进行逐级计算。

3. 对由质量算符M所定义的单粒子位阱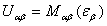进行了系统研究，证明了由它所确定的单粒子能量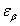严格等于满壳层基态与其相邻核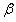态的能量差，其本征函数满足一类最大重叠原理，此单粒子位阱具有最佳的抵消性，是一种好的选择，常用的Hartree-Fock位是它的最低级近似。

4. 利用格林函数方法严格推导出了三维相对论性二体波动方程，给出了关于按Feynman规则进行计算的表达式，为相对论性波动方程的实际应用提供了一个好的理论框架。由此还推导出相对论性无规位相近似的严格谱表达式。 

四、吴式枢的主要论著

(1)吴式枢. 1951. 应用独立粒子模型讨论轻核的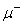捕获和光核反应. 美国Illinois大学博士学位论文.

(2)Wu S S. 1964. On a varitional method and the RP-HRP approximation. Scientia Sinica. 13: 9.

(3)Wu S S. 1965. Higher random phase approximation and the method of Green’s function. Scientia Sinica. 14: 377

(4)吴式枢. 1966. 推广的组态混合法. 中国科学 15: 773.

(5)吴式枢, 杨善德, 王明达. 1973 相位测井的物理基础. 吉林大学科学学报2: 57.

(6)吴式枢. 1973. 非线性积分方程与格林函数方法——粒子－空穴相互作用的无规位相（RPA）自屏蔽I. 中国科学 3: 255.

(7)吴式枢. 1974. 非线性积分方程与格林函数方法——粒子－空穴相互作用的无规位相（RPA）自屏蔽Ⅱ. 中国科学 5: 471.

(8)吴式枢, 姚玉洁. 1980多重散射理论与格林函数方法. 原子核物理 2:193.

(9)吴式枢. 1981.原子核的单粒子位阱理论. 中国科学 24:770.

(10)Wu S S. 1983 Principle of maximum overlap and optimal single particle potential. Commun. Theor. Phys. 2: 1059

(11)Wu S S, Kuo T. T. S  Effective integral equation and vertex operator of the Green’s function. Nucl. Phys. A 430 :110.

(12)Kuo T T S, Strottman D, Wu S. S. 1987. A systematic method for the calculation of temperature 2τGreen’s function. Nuclear Phase Transitions and Heavy Ion Reactions. ( World Scientific, Singapore 1987 ) 299.

(13)Wu Shishu. 1990. Three-dimensional relativistic two-body wave equation. J. Phys. G 16: 1447-1460.

(14)Wu S S, Yao Y J, Su J C, et al. 1992. A rigorous spectral representation of relativistic random phase approximation. Chin. Phys. Lett. 9:345-348.

(15)Wu S S. 1993. Retardation effect on baryon spectra. Chin. Phys. Lett. 10: 71-74.

(16)Wu S S. 1996. Concept of excessive mesons in nuclei. Chin. Phys. Lett. 13: 347-350

(17)吴式枢. 1998. 格林函数方法——等效相互作用与重整化. CCAST-WT Workshop Series. 95:1-30.

(18)Wu S S. Zhang H X, Yao Y J. 2001.Vector meson propagator and baryon current conservation. Phys. Lett. B 514: 33-40.

(19)Wu S S. Zhang H X, Yao Y J. 2001.Coupled Dyson-Schwinger equation and effect of self-consistency. Nucl. Phys. A 694: 489-510.

(20)Wu S S. Zhang H X, Yao Y J. 2006. Dirac Sea Contribution in Relativistic Random Phase Approximation. J.Phys.G. 32:1269-1277.

主要参考文献：

[1]J.S. Levinger. 1954. Theories of photonuclear reactions. Annu. Rev. Nucl. Sci. 4:13-32.

[2]《中国科学院院士自述》.1995. 中国科学院学部联合办公室编, 上海：上海教育出版社.

[3]Shen, L.C. 1985. Problems in dielectric-constant logging and possible routes to their solution. The Log  Analyst. 6:14-25

撰写者：

杨善德(1935~ )，36365线路检测中心教授，吴式枢先生的学生。